Indutância

[[Categoria:!Páginas a reciclar desde ]]

A Wikimotorpedia possui o portal: Portal de eletrônica {{{Portal2}}} {{{Portal3}}} {{{Portal4}}} {{{Portal5}}}

Eletromagnetismo
Representação do vetor campo elétrico de uma onda eletromagnética circularmente polarizada.
Eletrostática Carga elétrica Eletricidade Lei de Coulomb Campo elétrico Fluxo elétrico Lei de Gauss Potencial elétrico Potência elétrica Indução eletrostática Momento do dipolo elétrico Densidade de polarização Lei de Ohm
História História da Física
Magnetostática Lei de Ampère Corrente elétrica Campo magnético Magnetismo Magnetização Fluxo magnético Lei de Biot–Savart Momento magnético Polarização dielétrica Lei de Gauss para o magnetismo Força magnética
Eletrodinâmica Espaço livre Força de Lorentz Força eletromotriz Indução eletromagnética Lei da indução de Faraday Lei de Lenz Corrente de deslocamento Equações de Maxwell Campo eletromagnético Radiação eletromagnética Potenciais de Liénard-Wiechert Tensor de Maxwell
Circuitos elétricos Circuito elétrico Circuito RC Circuito RLC Circuito LC Frequência de ressonância Condução elétrica Resistência elétrica Capacitância Indutância Impedância elétrica Cavidade ressonante Guias de onda Fasor Capacitor
Físicos James Clerk Maxwell Heinrich Hertz Alessandro Volta Michael Faraday Charles de Coulomb Hans Christian Ørsted Nikola Tesla André-Marie Ampère Carl Friedrich Gauss Hendrik Lorentz

Em um sistema constituído de uma ou mais espiras, formando uma bobina perfeita - (resistência interna igual a zero) - quando percorrido por uma corrente elétrica produz um campo magnético, campo este que faz um fluxo <math>\Phi</math> que as atravessa.

Indutância pode ser definida como a razão entre o enlace total do fluxo e a corrente elétrica envolvida. Para o entendimento do conceito de enlace do fluxo, primeiramente consideremos um Toroide de N espiras , pelo qual uma corrente I que circula produz um fluxo total <math>\Phi</math>. O enlace de fluxo N<math>\Phi</math> é caracterizado como o número de espiras N presente no fluxo <math>\Phi</math>.

A capacidade de uma bobina de <math>N</math> espiras em criar o fluxo com determinada corrente <math>i</math> que percorre o circuito é denominada Indutância (símbolo L) medida em "henry" cujo símbolo é H.

<math>L=\frac{N \Phi}{i}</math>

Propriedades

A corrente num circuito produz um campo magnético e portanto, fluxo magnético. Assim, qualquer variação da corrente conduzirá a forças eletromotrizes induzidas no circuito.

Se, por exemplo, fecharmos um interruptor num circuito de corrente contínua, a corrente não aumenta instantaneamente desde zero até um valor final, devido à indutância do circuito. A tendência da corrente a aumentar bruscamente será contrariada por uma corrente induzida oposta, que regula o aumento da corrente de forma gradual. Igualmente, quando se abrir o interruptor a corrente não passará a ser nula de forma instantânea, mas de forma gradual.

Indutância mútua entre dois circuitos.

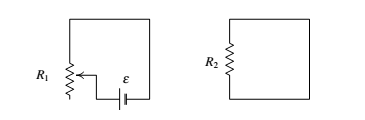
Imaginemos dois circuitos, um ao lado do outro (figura ao lado). No primeiro circuito está ligada uma pilha que produz uma corrente, existindo uma resistência variável que permite alterar a intensidade dessa corrente. No segundo circuito não está ligada nenhuma fonte.

A corrente no circuito 1 (lado esquerdo) produz fluxo magnético dentro do circuito 2, que deverá ser diretamente proporcional à corrente <math>I_1</math>, que produz esse campo magnético:

<math>\Phi_2 = -M\,I_1</math>

onde <math>M</math>é uma constante chamada (indutância mútua) , que depende da forma dos circuitos e da distância entre eles.

A variação da corrente no circuito 1 induz uma força eletromotriz no circuito 2:

<math>\varepsilon_2 = M\,\frac{d\,I_1}{d\,t}</math>

No sistema internacional de unidades, a unidade da indutância (volt vezes segundo, sobre ampere) é o henry, representada pela letra H.

Indutância Mútua

Estando dois ou mais circuitos próximos uns dos outros, como observado na Figura ao lado (circuitos elétricos adjacentes).

Circuitos Elétricos adjacentes. O fluxo magnético é resultante da soma de dois termos, sendo um proporcional a corrente do circuito 1 , e outro a corrente do circuito 2.

O fluxo magnético <math>\Phi</math> através de um circuito elétrico não depende somente da corrente naquele circuito, mas depende também da correntes dos outros circuitos correlacionados.

O campo magnético na superfície <math>S_2</math> é a superposição de <math>\overrightarrow{B_1}</math> referente a corrente <math>I_1</math> e <math>\overrightarrow{B_2} </math> devido a <math>I_2</math>. O fluxo magnético <math>\overrightarrow{B_1} </math> é proporcional a <math>I_1</math>, assim como <math>\overrightarrow{B_2} </math> é proporcional a <math>I_2</math>.

<math>\Phi_{m2,1}=M_{2,1}\,I_1</math>

No qual <math>M_{2,1}</math> é denominado de Indutância Mútua. O fluxo líquido <math>\Phi_{m2,1}</math> do campo magnético total <math>\overrightarrow{B}=\overrightarrow{B_1}+\overrightarrow{B_2}</math>, presente no circuito 2, pode ser descrito como <math>\Phi_{m2}=\Phi_{m2,2}+\Phi_{m2,1}</math>. Para o circuito 1, uma equação para o fluxo de <math>\overrightarrow{B_2}</math> é dado por:

<math>\Phi_{m1,2}=M_{1,2}\,I_2</math>

Com uma frequência alta, o fluxo magnético numa área contida num circuito varia com o tempo, devido as correntes de circuitos próximos que variam. A condição anterior induz uma força eletromotriz em um processo chamado de indução mútua, que depende da geometria dos circuitos e de sua orientação um em relação ao outro. A distancia de separação do circuito é inversamente proporcional a indutância mútua

O conceito de Coeficiente de indutância ( Indutância mutua), acontece quando da energia que ocorre da interação entre circuitos elétricos, sendo um fator que depende da geometria dos circuitos. O fator pode ser denominado de auto indutância quando se relaciona a auto-energia de um circuito e de indutância mutua quando a interação ocorre entre circuitos distintos.

Para um indutor a indutância pode ser calculada a partir da seguinte expressão:

<math> L= \frac{\mu_0.N^2.A}{l-0,45d}</math>

Onde:

- <math>\mu_0= 4.\pi. 10^-7(H/m)</math> é permeabilidade do vácuo;

-N e o número de espiras;

- l é a extensão da bobina;

- d é o diâmetro do núcleo;

- A é a área da secção transversal do núcleo;

Autoindução

Linhas do campo magnético produzido pela corrente num circuito.

Auto-indução lei de Faraday-Lenz

A corrente num circuito produz um campo magnético com linhas de campo que produzem fluxos de sentido contrário na área delimitada pelo circuito e no exterior do circuito (figura ao lado):

A lei de Faraday-Lenz descreve o fenômeno seguinte: quando o fluxo de um campo magnético que atravessa um circuito condutor varia ao longo do tempo, aparece neste circuito uma tensão chamada força eletromotriz. Lenz, afirma que a direção da corrente induzida é de tal forma que se opõe com seus efeitos magnéticos a causa que a produz.
Assim, a força eletromotriz induzida pode ser definida por:

<math> \epsilon_i =-\,\frac{1}{c}\,\frac{d\,\Phi_i}{d\,t} </math>

No qual o símbolo <math>\Phi_i</math> é caracterizado pelo fluxo no circuito , do campo <math>B_1 </math> devido a corrente <math>I_1</math>. O sinal menos indica que a força eletromotriz é sempre orientada a se opor a variação da corrente elétrica.

De acordo com a lei de Biot-Savart, o campo magnético produzido pelo circuito é diretamente proporcional à corrente. Portanto, o fluxo magnético produzido por um circuito sobre si próprio, e proporcional à corrente:

<math>

 \Phi =\frac{L}{N}\,I

</math>
A constante <math>L</math>é a autoindutância do circuito. A <math>fem</math> autoinduzida no próprio circuito é:

<math>

 \epsilon_i = -L\,\frac{dI}{dt}

</math>

Símbolo usado nos diagramas de circuito para representar a auto-indução.

Quanto maior for a área do circuito, maior será a sua autoindutância. Para evitar uma autoindutância elevada, que pode ser indesejada no caso de correntes variáveis, a fonte num circuito não se liga como na figura acima, mas com dois fios colados um ao lado do outro que ligam o dispositivo à fonte. Assim, reduz-se a área interna do circuito.

Nas partes do circuito onde se deseja que a indutância seja elevada, ligam-se bobinas com várias voltas e, portanto, com área interna elevada. Esses indutores representam-se nos diagramas de circuito com o símbolo da figura ao lado.

<math>L</math> representa o valor da indutância, medida em henries no sistema internacional. O símbolo da auto-indução total do circuito coloca-se em alguma parte do circuito. Na análise do circuito, esse dispositivo é designado de (indutor) e representa um elemento passivo em que a diferença de potencial é diretamente proporcional à corrente: <math>L\,dI/dt</math>.

Potência e Energia Armazenada em indutores

Um circuito sendo desligado, a corrente existente neste circuito pode variar induzindo uma corrente em outro circuito que esteja próximo. Quando uma corrente em um circuito esta aumentando, torna-se necessário um aumento da tensão induzida pela variação da corrente, aumentando-se a energia, que pode ficar armazenada e reaproveitada posteriormente. O indutor é capaz de armazenar energia em um campo magnético,sendo que um indutor quando percorrido por corrente elétrica, de acordo com a lei de Faraday ocorre um acúmulo de cargas positivas na entrada e de cargas negativas na saída de um indutor. O acumulo de cargas representa o armazenamento de energia no campo magnético. A energia pode ser dada por: <math>p(t)=\int_{t_0}^{t}Li(t).\frac{d_i(t)}{dt}\,dt= w-w_0</math>

com as condições iniciais nulas, temos: <math>w=\frac{1}{2}.Li^2(t)</math>