Ângulo
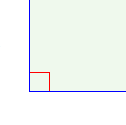
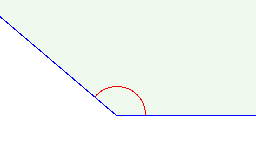
Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo[1]. A abertura do ângulo é uma propriedade invariante e é medida em radianos ou graus. Ângulo é um dos conceitos fundamentais da matemática, ocupando lugar de destaque na Geometria euclidiana, ao lado de ponto, reta, plano, triângulo, quadrilátero, polígono e perímetro[2].
Elementos conceituais, componentes e aplicações do ângulo
O principal ramo da matemática que se relaciona com o conceito de ângulo é a trigonometria. Além das funções trigonométricas, as principais funções (ou operações) com ângulos são a soma, a subtração e a multiplicação por um número[3].
Semirretas são os lados do ângulo. Origem ou vértice é o ponto onde as duas semirretas se encontram. Bissetriz é a semirreta com origem no vértice desse ângulo dividindo-o ao meio.
Ângulos consecutivos: dois ângulos são consecutivos se um dos lados de um deles coincide com um dos lados do outro ângulo. Ângulos adjacentes: Dois ângulos consecutivos são adjacentes se não têm pontos internos comuns.
Também é muito notória a conceituação dos números pi e e, ambas usadas nas operações e funções com ângulos.
Já na matemática aplicada é muito comum o uso de ângulos. Exemplos de ramos do conhecimento em que isto ocorre são a cartografia, a geografia, a engenharia, a física, a química, a biologia, vários ramos da medicina, como a ortopedia, a odontologia, a astronomia, a aviação.
Embora o senso comum preveja apenas ângulos positivos, a matemática admite a existência de ângulos negativos, ou seja, ângulos têm sinal. Tal questão é importante mormente no tratamento de vetores na forma polar, em alternativa à forma cartesiana.
Do mesmo modo, é definida na convenção matemática a noção de ângulos entre curvas, como sendo o ângulo entre as retas tangentes no ponto de interseção .
Unidades de medidas para ângulos
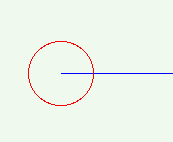
A medida em radianos de um ângulo é o comprimento do arco cortado pelo ângulo, dividido pelo raio do círculo[4]. O SI utiliza o radiano como a unidade derivada para ângulos. Devido ao seu relacionamento com o comprimento do arco, radianos são uma unidade especial. Senos e co-senos cujos argumentos estão em radianos possuem propriedades analíticas particulares, tal como criar funções exponenciais em base e.
A medida em graus de um ângulo é o comprimento de um arco, dividido pela circunferência de um círculo e multiplicada por 360. O símbolo de graus é um pequeno círculo sobrescrito °. 2π radianos é igual a 360° (um círculo completo), então um radiano é aproximadamente 57° e um grau é π/180 radianos.
O gradiano, também chamado de grado, é uma medida angular na qual o arco é dividido pela circunferência e multiplicado por 400. Essa forma é usada mais em triangulação.
O ponto é usado em navegação, e é definido como 1/32 do círculo, ou exatamente 11,25°.
O círculo completo ou volta completa representa o número ou a fração de voltas completas. Por exemplo, π/2 radianos = 90° = 1/4 de um círculo completo.
O ângulo nulo é um ângulo que tem 0°.
Medindo ângulos
Para medir um ângulo θ, um arco circular centrado no vértice do ângulo é desenhado. O comprimento do arco s é então dividido pelo raio do círculo r, e multiplicado por uma variavel k, que depende da unidade de medida selecionada (graus ou radianos). Se a unidade for radianos, k = 1; se a unidade for graus, <math>k \approx 57.29577951^\circ</math>.
- <math> \theta = \frac{s}{r}(k). </math>
Cabe mencionar que valor de θ é independente do tamanho do círculo (a proporção s/r é mantida), pois se o raio do círculo aumenta, o comprimento do arco também aumenta na mesma proporção.
Classificações dos ângulos
Quanto à medida
Com relação às suas medidas, os ângulos podem ser classificados como:
Nulo: um ângulo nulo mede 0°; agudo: ângulo cuja medida é maior do que 0° e menor do que 90°; reto: um ângulo reto é um ângulo cuja medida é exatamente 90°; assim os seus lados estão localizados em retas perpendiculares; obtuso: é um ângulo cuja medida está entre 90° e 180°; raso: ângulo que mede exatamente 180°, os seus lados são semirretas opostas; côncavo ou reentrante: ângulo que mede mais de 180°e menos de 360°; giro ou completo: ângulo que mede 360° (também pode ser chamado de Ângulo de uma volta).
O ângulo reto (90°) é um dos ângulos mais notórios e utilizados, pois o mesmo é encontrado em inúmeras aplicações práticas, como, aproximadamente, no encontro de uma parede com o chão, os pés de uma mesa em relação ao seu tampo, caixas de papelão, esquadrias de janelas, etc..
Um ângulo de 360 graus é aquele que completa o círculo. A volta completa coincide com o ângulo de zero graus mas possui a grandeza de 360 graus (360°). Tal identificação se assemelha à do ângulo negativo com o ângulo positivo que tem como medida exatamente aquele (negativo) somado com a volta completa.
Ângulos Consecutivos: dois ângulos são chamados consecutivos se um dos lados de um deles coincide com um dos lados do outro ângulo; ângulos adjacentes: Ângulos adjacentes são aqueles que possuem um lado em comum, mas as regiões determinadas não possuem pontos em comum; ângulos opostos pelo vértice: Dois ângulos são opostos pelo vértice quando os lados de um deles são semirretas opostas aos lados do outro.
Quanto a complementações
Ângulos complementares: dois ângulos são complementares se a soma de suas medidas é igual a 90°. Neste caso, cada um é o complemento do outro.
Ângulos suplementares: dois ângulos são Suplementares quando a soma de suas medidas é igual a 180°. Neste caso, cada um é o suplemento do outro.
Ângulos replementares: dois ângulos são Replementares quando a soma de suas medidas é igual a 360°. Neste caso, cada um é o replemento do outro.
Ângulos explementares: Dois ângulos são Explementares quando a diferença de suas medidas é igual a 180. Neste caso, cada um é o explemento do outro.
Histórico
Euclides definiu um ângulo plano como a inclinação entre duas linhas que se encontram em um mesmo plano. De acordo com Proclus, um ângulo deve ser uma quantidade, qualidade ou relação. O primeiro conceito (quantidade) foi usado por Eudemus, que via o ângulo como desvio de uma linha reta. O segundo conceito (qualidade) foi usado por Carpus de Antioch, que o via como intervalo ou espaço entre linhas intersecantes. Euclides adotou o terceiro conceito, no entanto, sua definição de ângulo reto, agudo e obtuso era claramente quantitativa.[5]
Um dos conhecidos três problemas clássicos da matemática grega foi o da trissecção do ângulo[6].
O Principia mathematica, um compêndio que tentou demonstrar do início os fundamentos da matemática, tinha um quarto volume previsto, especialmente para a geometria, mas que nunca foi realizado.
Significações derivadas
Existem vários significados para a palavra ângulo, todos eles derivadas da sua significação matemática, como ponto de vista, imagem que se vê através de uma lente e esquina[7]. Ângulo também pode significar o local no gol, em futebol, de onde se podem ver os noventa graus da trave, de difícil acesso ao goleiro e considerado local nobre para marcação do gol. "No ângulo" é a expressão da jogada exata.
Referências
- ↑ Viana, Giovana K. A. M; Toffoli, Sônia F. L.; Sodré, Ulysses. Ensino Fundamental: Geometria: Ângulos (em português). [S.l.: s.n.]. Página visitada em 11 de janeiro de 2012.
- ↑ {{#invoke:Citar web|web}}
- ↑ {{#invoke:Citar web|web}}
- ↑ {{#invoke:Citar web|web}}
- ↑ Heiberg, Johan Ludvig. Euclid (em inglês). [S.l.]: Cambridge University Press, 1908. vol. 1.
- ↑ {{#invoke:Citar web|web}}
- ↑ Ferreira, Aurélio Buarque de Holanda. Novo dicionário Aurélio da Língua Portuguesa (em português). 2 ed. Rio de Janeiro: Nova Fronteira, 1986. ISBN 8520904114
Ver também
Ligações externas